Následující kapitola : Gauss - Krügerovo zobrazení
1.4.3.1. Křovákovo zobrazení
Křovákovo zobrazení je dvojité kuželové konformní zobrazení v šikmé poloze, převádějící Besselův elipsoid do roviny prostřednictvím referenční koule (Cap 1992). Navrhl jej ing. Josef Křovák v roce 1922. Na našem území se používá od r. 1938 (s přerušením během II. světové války a 50. a 60. let 20. stol., kdy se Základní mapy (ZM) velkých měřítek vyhotovovaly přednostně v Gaussově zobrazení s třístupňovými poledníkovými pásy.)
Křovákovo zobrazení je základem pro souřadnicový systém S-JTSK.
Výpočet zobrazení je mimořádně komplikovaný, protože v sobě zahrnuje několik kroků, které je možné napsat zkráceně takto:
- Konformní zobrazení Besselova elipsoidu na kouli (Gaussovo zobrazení) s jednou nezkreslenou rovnoběžkou (49°30´)
- Definování soustavy kartografických souřadnic Š,D - kartografický pól K je umístěn asi 24°50´ východně od Greenwiche, φk je asi 59°45´. Transformace souřadnic U,V na Š,D.
- Konformní zobrazení koule na kužel
- Převod polárních souřadnic na pravoúhlé - počátek souřadnic je umístěn do vrcholu kužele a osa X do přímkového obrazu poledníku λk
Křovák při odvozování zobrazovacích rovnic použil úvahy, že požadovaného délkového zkreslení základní rovnoběžky dosáhne i zmenšením poloměru kartografické koule na hodnotu r*0,9999 ještě před před vlastním zobrazením koule na kužel. Základní zobrazovací rovnoběžce Š0 bylo přisouzeno délkové zkreslení m0 = 0,9999. Tím se celé řešení mění na zobrazení se dvěma nezkreslenými rovnoběžkami – dospělo se tím téměř eliminace délkového zkreslení při konformním zobrazení.
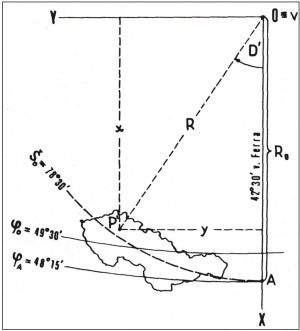
Obr.4.3 Pravoúhlá soustava souřadnic v Křovákově zobrazení (Upraveno podle: Srn 1986)
V rovině Křovákova zobrazení je zeměpisná síť vyjádřena křivkami vyšších řádů. V rozsahu území ČR (a bývalého Československa) je prakticky možno zobrazovat zeměpisné poledníky na mapách jako přímky a zeměpisné rovnoběžky jako soustředné kružnice (Srn 1986).
Z hlediska zkreslení je Křovákovo zobrazení vhodné jen pro území ČR a Slovenska, popř. pro úzký pruh území rozložený podél základní rovnoběžky Š0. Již ve vzdálenosti 200 km na obě strany od této rovnoběžky vzniká zkreslení +0,5 m / km a s dalším zvětšováním vzdálenosti rychle vzrůstá (Srn 1986).
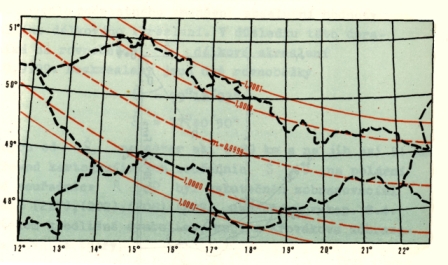
Obr.4.4 Délkové zkreslení v Křovákově zobrazení (Upraveno podle: Srn 1986)
Následující kapitola : Gauss - Krügerovo zobrazení

