Následující kapitola : UR�OV�N� POLOHY BOD� NA STAR� MAP�
4.2.3. ZJIŠŤOVÁNÍ MĚŘÍTKA STARÉ MAPY
p> U nejstarších map většinou vůbec nelze určit měřítko, v těchto přídech ho často nahrazujeme údajem o zobrazeném území a formátech pokreslovací podložky (velikosti klu, kosti, hliněné destičky, pergamenu, papíru apod.). Mapy konstruované v období od 14. do 19. století obsahují měřítka především grafická a slovní, a to v jedné nebo více různých dobových mírách (obr.4.3). Kromě délkových měr, např. mílí, byly užívány i míry, které představovaly dráhu, kterou lze urazit pěšky, na koni, slonu apod. za časovou jednotku (hodnota této míry se např. měnila podle uvažované délky kroku a rychlosti, kterou se měřič pohyboval). Číselné měřítko 1:M převládlo na mapách teprve v průběhu 19. století.Není-li měřítko na mapě uvedeno, zjišťuje se pomocí jiných metod. Pro exaktnější zjištění, případně pro kontrolu, je vhodnější použít alespoň dvě rozdílné metody na staré mapě.
Výpočtem ze slovního měřítka:
Zde je nutné znát buď poměry starých měr nebo přesné převody starých měr na metrickou míru. Ukázka slovních záznamů na mapách ve stejném měřítku map odvozených z generálních map II. vojenského mapování:
-
"Masstab der Wiener Zoll gleich eine Oesterreichische Post Meile" (tj. jeden vídeňský palec na mapě rovná se jedné rakouské poštovní míli ve skutečnosti),
"Oesterreichische Postmeilen zu 4000 Wr. KL. oder ein Wiener Zoll" (tj. rakouská poštovní míle po 4000 vídeňských sázích nebo jeden vídeňský palec - volně přeloženo - obr.4.4),
"1 Zoll ´1 Oester. Postmeile oder 4000 Klafter der Natur" (tj. 1 palec = rakouská poštovní míle nebo 4000 sáhů ve skutečnosti),
"1 Wr. Zoll = 4000 Wr. Klafter" (tj. 1 vídeňský palec = 4000 vídeňských sáhů),
- a)Výpočet ze známých poměrů starých měr: - Příklad: 1 Wr. Klafter = 1o = 72 Wr. Zollen = 72" 1: M = 1": 1 Oester. Postmeile = 1": 4000o = 1: 72x4000 = 1: 288 000 měřítko mapy = 1: 288 000 (výpočet odpovídá přesně poměru měřítka mapy).
- b)Výpočet převodem starých měr na míru metrickou: - Příklad: 1 Wr. Zoll = 1" = 26 mm, 1 Oester. Postmeile = 7,6 km (zaokrouhlené hodnoty) 1: M = 1 mm (na mapě): 1 Postmeile / 1" = 1: 7 600 000 / 26 = 1: 292 307,692 (asi 2920308) měřítko mapy = 1: 292 308 (výpočet je zaokrouhlením zkreslený) - Příklad: 1 Wr. Zoll = 1" = 26,340 1 mm, 1 Oester. Postmeile = 7,585 936 km (nezaokrouhlené hodnoty) 1: M = 1 mm: 7 585 936,0 / 26,340 1 = 1: 287 999,514 ( zaokrouhleně 1: 288 000) měřítko mapy = 1: 288 000 (výpočet odpovídá přesně poměru měřítka mapy).
Měřítko mapy odvozené z generální mapy II. vojenského mapování je skutečně 1: 288 000.
Určením z grafického měřítka:
Výpočtem z délky úsečky grafického měřítka popsaného jednotkami starých délkových měr, event. doplněných slovním zpřesněním; pro příklad je použita Bayerova mapa Moravy a Slezska z roku 1818, na které jsou tři transverzální (příčná) měřítka, a to pro geografické, poštovní a moravské míle:
- a)Výpočet z příčného měřítka pro geografické míle: "Masstab von 5 geographischen Meilen deren 15 auf einem Grad eines grössten Kreises gehen." Délka úsečky 5 geografických mil = 19,39 mm výpočet: 1 geografická míle = 1/15 stupně na rovníku = 7,420 438 5 km M (měřítkové číslo) = 5 geografických mil : délkou úsečky na mapě M = 5 x 742 043,85 : 19,39 = 191 347,04 měřítko mapy zaokrouhleně = 1: 191 350
- b)Výpočet z příčného měřítka pro geografické míle: "16 000 Wiener Klafter oder 4. Postmeilen." Délka úsečky 4 poštovních mil = 15,62 mm výpočet: 1 poštovní míle = 4 000 vídeňských sáhů = 7,585 936 km M (měřítkové číslo) = 4 poštovní míle : délkou úsečky na mapě M = 4 x 758 593,60 : 15,87 = 191 201,91 měřítko mapy zaokrouhleně = 1: 191 200
- c)výpočet z příčného měřítka pro moravskou míli: "Masstab von 3 mähris. Landmeilen wovon 10.3/4 auf einem Grad eines grössten Kreises gehen." (obr.4.5). Délka úsečky 3 moravských mil = 16,27 mm výpočet: 1 moravská míle = 1/10 3/4 stupně na rovníku = 10,354 099 km M (měřítkové číslo) = 3 moravské míle : délkou úsečky na mapě M = 3 x 1 035 409,9 : 16,27 = 190 917,62 měřítko mapy zaokrouhleně = 1: 190 920
Podle těchto výpočtů má Bayerova mapa Moravy a Slezska z roku 1818 ve všech třech případech na měřeném exempláři z fondu Geografického ústavu MU v Brně inv.č. B-502/580 má měřítko mapy přibližně 1: 191 000 (v literatuře uváděno měřítko 1: 192 000), což se velice zhruba blíží ve II. vojenském mapování používaném poměru 1: 194 400.

Obr. 4.3. Ukázka grafických měřítek ze Sansonova atlasu z roku 1695

Obr. 4.4. Ukázka slovního a příčného měřítka na mapě odvozené z II. vojenského mapování

Obr. 4.5. Ukázka příčných měřítek z Bayerovy mapy Moravy a Slezska z roku 1818
Použitím nomogramu:
Nomogram je pomůcka k určování k určování číselného měřítka mapy z údajů měřítka grafického, to znamená z délky měřítka v cm (event. mm) a počtu udaných km (event. mil apod. převedených na km) a anglických statutárních mil, případně zeměpisných stupňů, které měřítko znázorňuje. Nomogram je většinou sestrojován pro určování středních a malých měřítek cca 1: 250 000 až 1: 50 000 000 (obr.4.6).
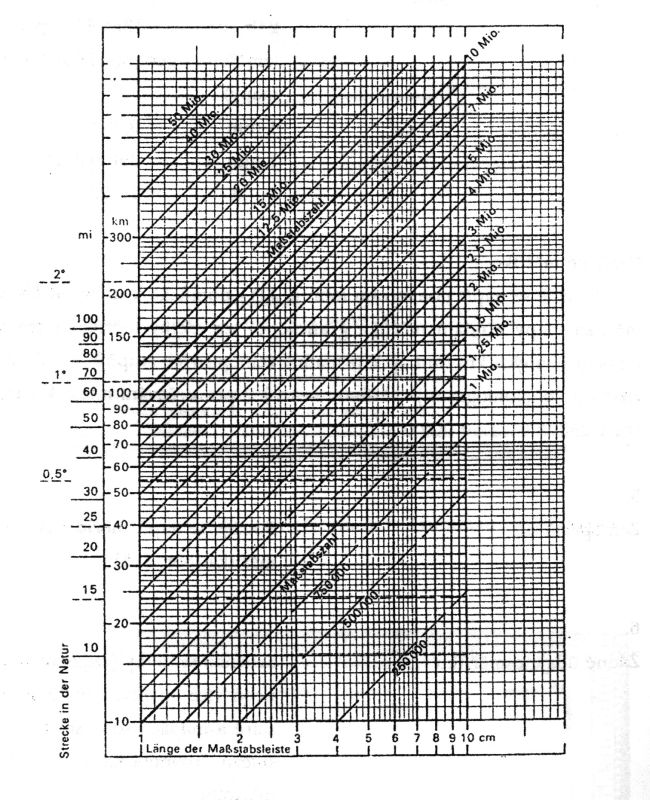
Obr. 4.6. Nomogram podle G. RENNAU 1972
Určení měřítka ze zákresu zeměpisné sítě:
Na starých mapách většinou až do druhé poloviny 18. století se s různou přesností vycházelo z jiných rozměrů Země, než jaké známe po zavedení metrické míry. Vycházelo se především z údajů Poseidonia (137-50 př.n.l.) který určil velikost kvadrantu Země na 8 333 100 m, a to přesto, že daleko přesnější byly údaje od staršího měření Eratosthena z Kyréne (276-195 př.n.l.), který podle novodobých propočtů určil délku kvadrantu Země na 9 922 500 m, což se blíží správné hodnotě.Nebyly využívány ani daleko přesnější rozměry země, které byly zjištěny již na počátku 16. století lékařem Fernelem a po něm dalšími. To znamená, že délka 1° zeměpisné šířky byla tehdy zpravidla přibližně 92,60 km. Od Fernelova prvního stupňového měření v Evropě 1525 a dalších (Schnelia 1610-1615 a Norwoodova 1636) byl 1° z.š. přibližně 111 km, od druhého stupňového měření francouzské akademie 1791-1808, kdy délka kvadrantu Země byla stanovena na 10 000 000 m (počátek metrické míry), byla délka 1° z.š. stanovena na 111,111,km, při tom délka 1° z.d. po rovníku byla 111,307 km.
Současně je důležité si uvědomit, že zákres zeměpisné sítě zpravidla až do konce 18. století se prováděl nezávisle nebo dodatečně po kresbě obsahu v mapovém poli a netvořil ani geometrický ani geodetický základ map. Proto je vhodné u starých map uvádět jak měřítko podle zeměpisné sítě, tak i měřítko podle kresby obsahu mapy.
- a)Určení měřítka cejchovaným měřidlem: Zjištění číselného měřítka provádíme na cejchovaném měřidle, zhotoveném na průsvitné folii. Po jeho přiložení k dělení zeměpisné sítě po poledníku, zpravidla na levém okraji rámu mapy, přímo odečteme délku co nejpřesněji v desetinách, resp. setinách mm. Spolehlivost odečtu na cejchovaném měřidle je u nestandardních měřítek pouze orientační.
- b)Výpočet měřítka z minutového a stupňového dělení zeměpisné sítě:
Při tomto kartometrickém šetření vycházíme z poměru skutečné délky 1° z.š. na zemi ku délce 1° z.š. změřené po poledníku na mapě:
- Příklad (opět Bayerova mapa Moravy a Slezska 1818): skutečná délka 1°z.š. = 111,111 km, délka 1° z.š. na mapě = 57,27 cm 1: M = 1: 1° z.š. skuteč. / 1° z.š. mapa = 1: 111 111 / 0,5727 = 1: 194 012,57
měřítko mapy zaokrouhleně 1: 194 010
Zjištěné měřítko mapy 1:194 010 je zhruba jako měřítko podle příčných měřítek, ale daleko více se blížící hodnotě 1:194 400.
Určením měřítka podle kresby obsahu mapy:
Tento způsob se užívá hlavně na starých mapách rukopisných nebo vytištěných do doby, než se mapy začaly konstruovat na geodetických základech, tzn. přibližně do počátku 19. století. Na pozdějších mapách se tento způsob užívá pouze orientačně k vyloučení chyby při zjišťování měřítka, která mohla vzniknout z aplikace nesprávného uvedení hodnot při popisu zeměpisné sítě nebo grafickégo měřítka mapy. Na příklad na Bodenehrově mapě Moravy asi z roku 1720 je správně popsána rovnoběžka 49° z.š. svou hodnotou, ovšem místo chybně vyryté hodnoty 50° z.š. měla být správně hodnota 49°40'. Potom prostý výpočet měřítka podle zákresu zeměpisné sítě na této mapě s uvedenými hodnotami 49° a 50° je chybný, vypočtené měřítko 1: 1 012 000 by po opravě vyšlo 1: 680 000.
Při tomto způsobu se vzdálenosti dvojic bodů změří na moderní mapě (nejlépe v měřítku 1:1 000 000 nebo 1: 100 000) nebo vypočtou skutečné vzdálenosti na zemském povrchu např. ze zeměpisných souřadnic. Potom změříme vzdálenosti mezi stejnými dvojicemi bodů na staré mapě. Měření vzdáleností provádíme s maximální přesností např. vynášecí soupravou alespoň na 0,01 mm. Volí se minimálně jedna dvojice přibližně ve směru poledníkovém a jedna dvojice ve směru rovnoběžkovém.
Čím starší je doba vzniku staré mapy, tím více párových dvojic se snažíme vyhledat, změřit vzdálenosti a porovnat. Současně, čím starší je studovaná mapa, tím je také menší spolehlivost při odvozování výsledného měřítka mapy. Potom větší váhu dáváme měřítkům vypočítaných z dvojic bodů v poledníkovém směru a současně dvojicím bodů významnějších lokalit. Z vypočtených měřítek většinou provedeme vážený aritmetický průměr.
Při vyhledávání bodů zjišťujeme především místa - sídla, která v době vyhotovení mapy byla již astronomicky určena nebo uvedena v textových itinerářích, tabulkách souřadnic bodů, případně která leží na starých dálkových cestách, např. císařských silnicích nebo poštovních trasách, které mívaly udávány vzdálenostní údaje, při soutocích řek apod.
- Příklad (opět na Bayerově mapě Moravy a Slezska z roku 1818):
zvolené dvojice: Brno-Moravská Třebová (směr S-J), Jihlava-Kroměříž (směr Z-V) a kontrolní dvojice dvou velkých měst Brno-Olomouc (směr JZ-SV)
měřítko mapy udává poměr skutečné vzdálenosti ku vzdálenosti na mapě:
| dvojice sídel | skutečná vzdálenost | vzdálenost na mapě | poměr - měřítko |
| [km] | [mm] | ||
| Brno-Moravská Třebová | 64,0 | 32,95 | 1: 194 233,68 |
| Jihlava-Kroměříž | 131,5 | 69,50 | 1: 189 208,63 |
| Brno-Olomouc | 66,5 | 34,40 | 1: 193 313,95 |
Z výpočtů poměrů vzdáleností zjišťujme, že číselné měřítko ve směru S-J zaokrou-leně 1: 194 230 je blízké měřítku vypočtenému z 1°z.š. 1: 194 010 a později užívanému sáhovému měřítku 1" (na mapě) = 2 700? (ve skutečnosti) = 1: 194 400, kdežto ve směru Z-V měřítko zaokrouhleně 1: 189 200 je bližší výpočtům podle příčných měřítek na Bayerově mapě Moravy a Slezska z roku 1818 v průměru 1: 191 000. To znamená, že mapový obraz je protažen ve směru Z-V. Z těchto zjištění také vyplývá, že příčná měřítka byla zřejmě na této mapě konstruována v závislosti na zobrazovací rovnoběžce. Příčinu tohoto protažení v rovnoběžkovém směru bude tedy třeba hledat a zjišťovat při určování kartografického zobrazení a ekvideformát, případně kvaziekvideformát.
Pokud zjistíme větší variabilitu měřítek v mapovém poli, může mít hodnocená stará mapa více lokálních měřítek. V tom případě rozdělíme mapu na segmenty, např. na čtvrtiny, a v každém segmentu provedeme samostatné měření nejméně dvou dvojic bodů jak v poledníkovém, tak rovnoběžkovém směru.
Závěrem lze u určování měřítek mapy poznamenat, že pokud se zjištěná měřítka podle různých metod výrazněji liší, je nutné uvést každé měřítko a popsat, podle jaké metody bylo zjištěno.
Tak na příklad měřítko mapy Moravy od J. A. Komenského, typ KMM P poprvé vydané roku 1624, má podle 1° s.š. zeměpisné sítě, zakreslené na levém okraji mapového rámu, hodnotu zaokrouhleně 1: 480 000, podle kresby obsahu mapy zaokrouhleně 1: 530 000. Problematické by bylo zjištění měřítka na této mapě ještě podle grafických měřítek, protože přesné rozměry obecné např. moravské míle z té doby neznáme.
Předcházející kapitola : ZJI��OV�N� KVAZIEKVIDEFORM�T
Následující kapitola : UR�OV�N� POLOHY BOD� NA STAR� MAP�

